A seemingly unrelated counting problem

We’ll start our journey with the following puzzle:

Given is a $n \times m$ grid. The cell in the $i$th row and $j$th column is denoted as $(i, j)$. Count the number of paths from $(1,1)$ to $(n,m)$ if the only possible moves from a cell are move to the right or move below.

It is recommended to ponder the problem for some time before moving on.

Solution by counting

The first solution to the problem is quite elementary. There is a more novel (and faster to compute) solution which will be presented later but the more elementary solution is the basis of the derivation. The crucial observation here is that for any cell $(i, j)$ where $i > 1$ and $j > 1$, you can go to it from either $(i - 1, j)$ or $(i, j - 1)$ and any path that contains the cell $(i - 1, j)$ cannot contain $(i, j - 1)$. Hence, all the paths to $(i - 1, j)$ are different from all the paths to $(i, j - 1)$! This means that the total number of paths to $(i, j)$ is simply all the ways you can come to it from $(i - 1, j)$ plus all the ways you can come to it from $(i,j - 1)$. 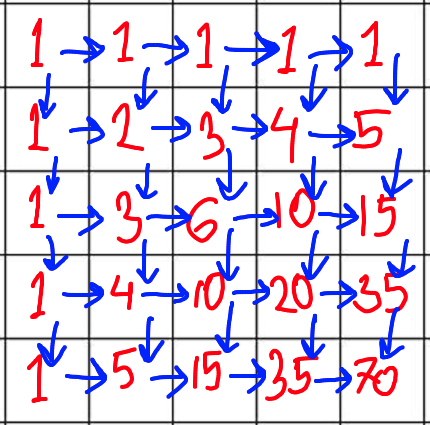Notice that all the cells at the sides have only 1 way to come to them, which is intuitive enough.

More formally, let $f(i, j)$ be the number of paths to cell $(i, j)$. We can recursively define this like so: $$f(i, j) = \begin{cases} f(i - 1, j) + f(i, j - 1) & \text{if $i > 1$ and $j > 1$} \\ 1 & \text{otherwise} \end{cases}$$

A more novel solution

Changig our perspective significantly slightly, we can observe that each path from cell $(1, 1)$ to cell $(i, j)$ can be described as a sequence of $i - 1$ Rs (R for right) and $j - 1$ Ds (D for down) in some order. Framing the problem this way, it becomes apparent that the number of paths to $(i, j)$ is simply the number the of ways to choose positions for the Rs (the D positions will be fixed after choosing the R positions). Let $g(i, j)$ be the answer for going from $(1, 1)$ to $(i, j)$. Therefore we have $$g(i, j) = {i - 1 \choose{i + j - 2}} = {j - 1 \choose{i + j - 2}}$$ There are $i - 1$ Rs and the total path length is $i - 1 + j - 1$

Equivalence

Now that the fun puzzle is solved, we are equipped to connect the dots. Obviously, $f(i, j) = g(i, j)$. But notice the similarity between the counting solution and the way each number of pascal’s triangle is obtained. It’s actually the same! Rotating the above figure 45 degrees clockwise and laying it on the triangle, we get the following: 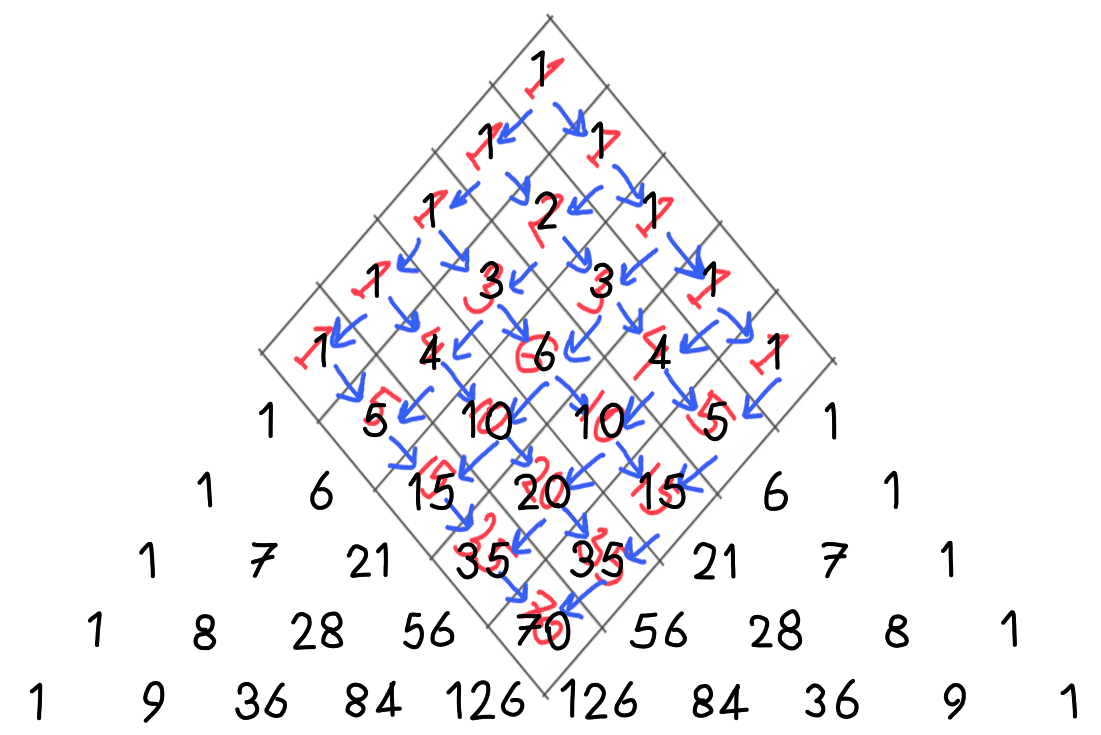As can be seen from the picture, for getting to the 9th row and 5th column of the triangle, a $5 \times 5$ grid can be constructed. For the number in row $r$ and column $c$ of the triangle, a $r + 1 - c \times c$ grid can be constructed. And so the problem of “find the number in row $r$ and column $c$ in pascal’s triangle” can be completely translated into the problem stated at the top of this page.